“量子”北大校友将量子信息暴散用于计量学,通过直观方式观察量子纠缠,可用于提高精密测量的准确度
今天,很高兴为大家分享来自DeepTech深科技的北大校友将量子信息暴散用于计量学,通过直观方式观察量子纠缠,可用于提高精密测量的准确度,如果您对北大校友将量子信息暴散用于计量学,通过直观方式观察量子纠缠,可用于提高精密测量的准确度感兴趣,请往下看。
来源:DeepTech深科技
北大本科校友、MIT 博士、斯坦福博士后,这是北京男孩李泽阳身上的三个标签。
 业余,他还喜欢说相声。更让人感到与众不同的是,前不久在自己的 Science 一作论文里,他直接把中文名字写在了作者栏。
业余,他还喜欢说相声。更让人感到与众不同的是,前不久在自己的 Science 一作论文里,他直接把中文名字写在了作者栏。目前,李泽阳正在斯坦福大学做博后研究。不久之后,即将开始寻找教职。他表示:“我对于回国工作非常感兴趣。目前国内在冷原子领域的发展令人感到很兴奋,无论是在沿海发达城市还是内陆工业重镇都能看到一些冷原子课题组的卓越工作。如果条件允许我非常希望能够在国内开展我的后续研究。”
那么李泽阳此次发表的 Science 论文,到底讲了什么?Science 期刊编辑在点评文章中提到:“李博士等人将局部量子信息快速分布在系统的众多自由度中,这一技术可以用来提高精密测量和传感。”
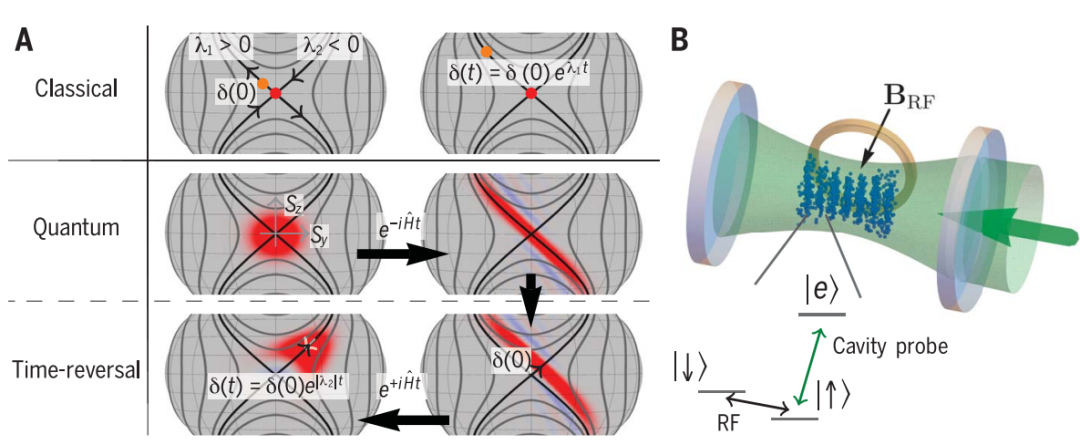 (来源:Science)
(来源:Science)而要讲清楚背后的意义,还得从量子纠缠说起。量子纠缠,是一个既神秘又令人激动的领域。从爱因斯坦时代对量子纠缠的存在与否的质疑;到数十年前对量子纠缠能否带来比经典计算更优的各种应用;再从研究者到平民百姓,人们对于量子纠缠的讨论从未停歇。对于科学家来说,如何能用量子现象达到比经典系统更加优异的表现则是其中的重点。
量子计量学则是量子纠缠里的一个特殊研究方向,旨在利用量子纠缠来达到比经典系统更高的测量精度。量子涨落,则是其中涉及到的一个重要概念。由于量子涨落的存在,绝大多数针对物理量的测量都会存在一定误差。多数时候,这个误差被称为散粒噪声,它来自于观测量载体本身的读数所对应的量子化。而对于无量子涨落的系统,则称之为标准量子极限。
自 2010 年开始,MIT 教授弗拉丹·弗莱蒂奇(Vladan Vuletić)课题组就开始尝试利用量子纠缠突破经典量子极限来做测量。具体来说,他们在实验中生成了一个确定的哈密顿量——单轴扭曲(One-Axis Twisting, OAT)。为了让这一实验不只是纸上谈兵,2020 年该团队着重于将量子纠缠应用于光钟,并发表了一篇具有里程碑意义的论文 [2]。
李泽阳也参与到了这一论文当中。打那时起,他一直思考的是虽然这种办法的确使用了量子纠缠。但是,一方面这仅仅使用了某一种特殊形式的量子纠缠。而且,过程之中纠缠的制备也非常慢。
在量子计算中,很多时候所谓的“加速”,其实都会用到量子的指数多的性质。那么,能否把两者结合起来?
调研之中,李泽阳和同事发现很多其他相互作用形式所产生的纠缠性质,都可以用非时间序关联函数来测量。关键在于,要找到一个有正 Lyapunov 指数的“混沌”系统,并对其进行微扰后的时间反演。
对于前者来说,可以通过将常用的纠缠哈密顿量 OAT 加入额外的一项形成 LMG 哈密顿量来实现;对于后者来说,恰好会使用到李泽阳所在课题组发展出来的一项名为时间反演的新技术 [3]。
基于此,该团队以 LMG 哈密顿量为例,用时间反演为手段,展现了一种他们认为比较普适的方案:即利用量子信息里面的快速纠缠制备来提供量子计量,最终在 LMG 哈密顿量上取得了不错的成果。另外,本次研究是在非常可控的实验中完成的,因此审稿人评价称“将给计量学带来惊人的影响”。
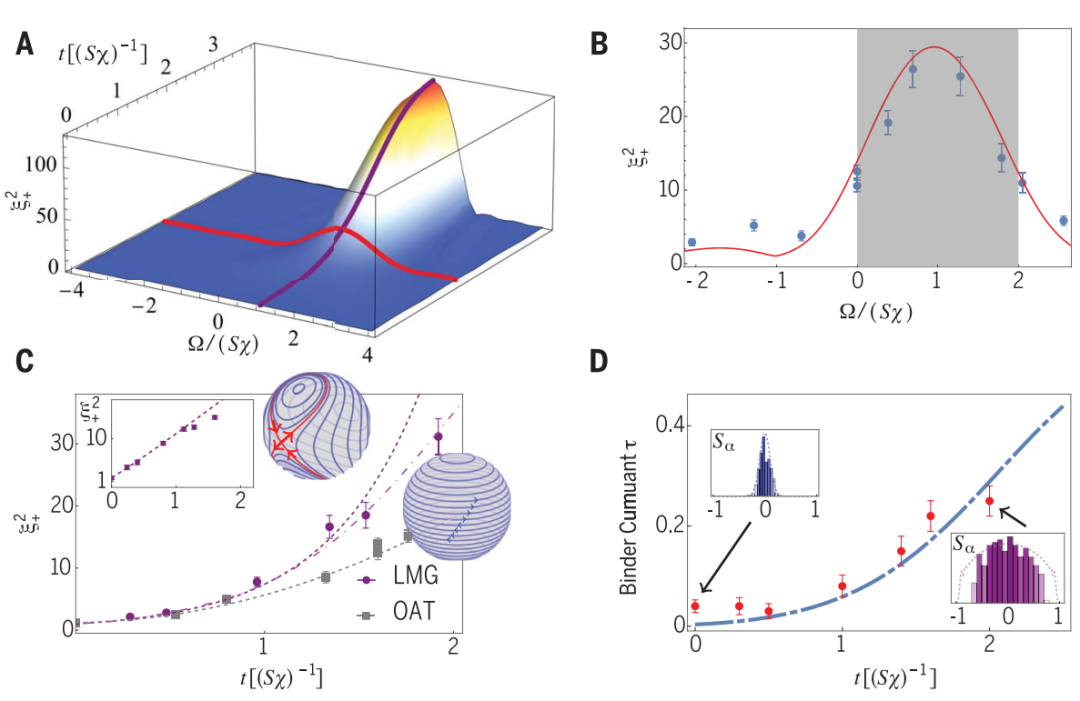 (来源:Science)
(来源:Science)事实上,李泽阳最初要做的并不是这个课题。最开始,他打算做另一个课题。后来,课题组突然发现一些类似于相变的奇怪现象。对于这一现象来说,在数值上很容易得到重复,但却很难从物理角度对其进行解释。最开始他们尝试从量子相变角度来理解。
遗憾的是,无论从数值上还是实验上,都无法在已有参数区间之内很好地看到这个角度。后来,该团队想到了经典非线性系统的分岔,于是将其与经典的混沌系统联系起来,来作为研究一类量子混沌的手段。
李泽阳表示:“最终我们确定按照这个方向是在 2021 年底。当时,我们进行了包含多位教授在内的一个大讨论,那晚开会开到十点多,波士顿的冬天晚上黑得非常早,整层楼只有我们的屋子是亮的。讨论到后面那种感觉非常像廉价恐怖片的片场。不过散会之后,大家都嘻嘻哈哈的,因为对这个实验非常有信心。”
然而,实验难度比想象中要难得多,LMG 哈密顿量确实能在一些系统中实现,这些系统可以是带自旋的玻色-爱因斯坦凝聚,可以是离子阱的振动模式驱动,可以是腔量子电动力学,可以是人工的玻色双格点,也可以是约瑟夫森结等。但这些方案都要么很难时间反演,要么时间反演很难做到严格准确。为此,李泽阳专门为这个实验开发了一套双频率驱动光学腔的办法,借此解决了不均匀的相位退相干问题。
同时,他们咨询了瑞士巴塞尔大学教授罗曼·施密德(Roman Schmied),并学习如何进行有效的态重构。“在这两个技术的帮助之下,我们把数据处理得非常成功,这让我们能用非常直观的方式看到纠缠的影响。”李泽阳说。
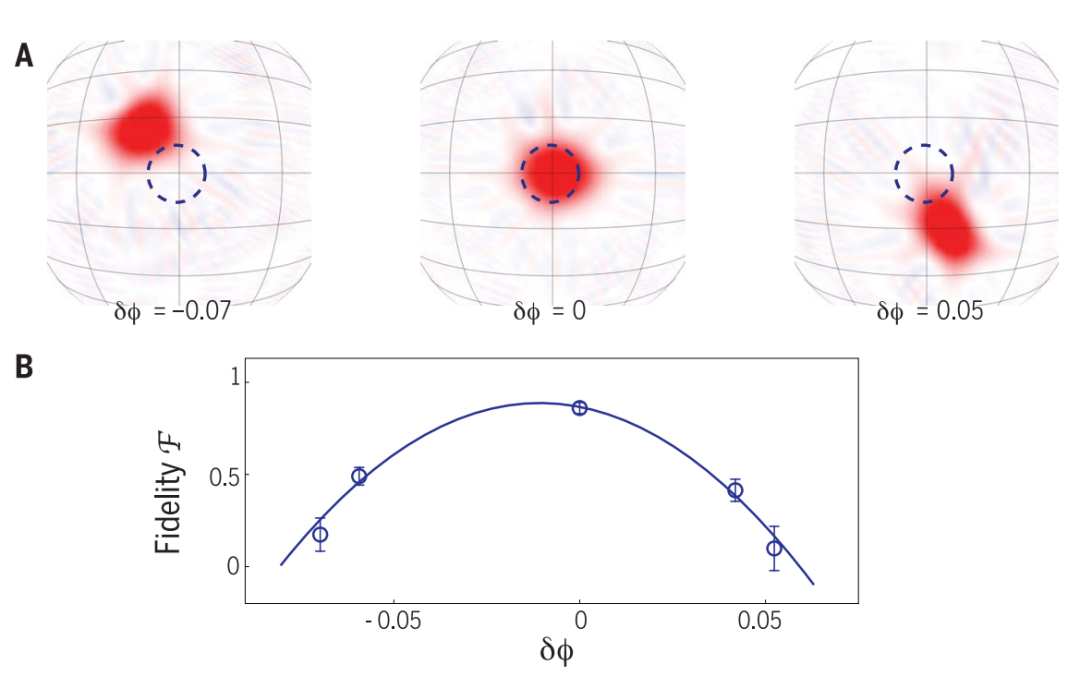 (来源:Science)
(来源:Science)2021 年,在一场原子分子光学领域的大会上,李泽阳在演讲中介绍了此次工作的前身——也就是此前被放弃的课题。
等到 2022 年,尽管李泽阳在研究中使用的还是同一个系统,但是更换了参数和研究角度。没想到在 2023 年论文发表之后,竟然有人看出来了。对此他表示:“这让我感觉挺好的,看起来这个工作有一定影响力。”
目前,量子计量已经非常接近于真正地走进实际应用。李泽阳表示:“如果五年前,我会说量子测量几乎是唯一一个能在十年内看到应用的量子技术。当然,这些年的量子计算和量子通讯的发展也确实显得勃勃生机万物竞发,所以我的上述观点显然有点武断。”
不过,科技前沿成果的直接应用,当然还是用于科研本身。目前很多基于一类室温量子材料比如 NV 色心的量子传感,已被用于测量各种微弱的电磁学信号。
另一方面,光原子钟技术的进步已经逐渐放缓,因此利用量子计量来提高原子钟的精度是领域内的目标。哪怕不是为了追求最高的精度,人们也希望能够使用便携的原子钟,来通过简单的纠缠制备去提供更好的表现性能。
一些非常重要的应用比如定位系统(GPS、北斗等),其原理都是通过多颗卫星高精度地广播自己的坐标和时间,借此来推定接收信号的点的坐标。如此一来,时间精度直接转化为位置精度,从而给定位和导航带来极大帮助。
而在接下来,针对更一般的相互作用,李泽阳将开展一些新研究,并将它们与量子少体、量子多体混沌联系起来。
物理,是李泽阳从中学起就开始打交道的专业。高中时李泽阳通过物理竞赛保送至北京大学物理学院读本科,大学期间发表了几篇关于光学腔的论文,后来到 MIT 攻读直博。
李泽阳表示:“MIT 是一个非常神奇的地方,我非常感谢我在这里受到的教育,也从 MIT-哈佛联合冷原子中心的各位导师那里受益颇丰。”
但是,MIT 的实验条件是比较“艰苦”的。例如,精密测量实验竟然紧挨着电梯,光是电梯上上下下就会对实验产生巨大影响。
不仅如此,李泽阳所在的实验室距离地铁特别近,白天的磁场噪声非常大,直到晚上地铁停运之后才会好转。为此,有时做实验不得不在深夜采集数据。
在 MIT 获得博士学位之后,李泽阳来到斯坦福大学从事博后研究。“我在斯坦福的博后指导导师 Jonathan Simon 也毕业于 MIT-哈佛联合冷原子中心,他的评价是在 MIT 的那一栋楼里,一切令人激动的实验进展都是不可思议的,因为他深切地知道会面临着多么巨大的挑战。”
课余之外,李泽阳非常喜欢说相声。作为一名北方人,打小就听过一些相声。后来,他发现在 MIT 有一个由前辈们(也是物理 PhD,甚至有一位前辈也毕业于 MIT-哈佛联合冷原子中心)创立的相声社,迄今成立已有 12 年。
一开始,李泽阳只是作为一个票友随便听听。后来,机缘巧合之下他们邀请李泽阳一起参加排练、以及演出后的反思会。逐渐地,他也诞生了演出的想法。
其表示:“我们说的相声大部分是基于传统段子的改编。比如说我最近演出了《大保镖》,原本的设计是让逗哏演员假装是一个武术家,然后通过各种说漏嘴出洋相来制造对比。但是,传统段子里面的设计对于现在的观众尤其是海外观众不是很友好,于是我就做了一些本地化。”
比如说,原本的台词里有这样一句话“京西北宣平坡下坎儿有个地方叫虎岭”。这个地名其实是以讹传讹的,而且这个地方盛产粽子而不是武术。
然而,除了京津冀一带的人应该根本 Get 不到,于是李泽阳就改成了“波士顿西北哈佛商学院下坎有个地方叫全(拳)镇”。因为哈佛商学院确实在波士顿西北,那个地方叫 Allston,all 也是全(拳)的意思,并且也因餐馆良多出名。对于此次演出的台词,李泽阳做了不少类似改动,观众反应都比较不错。
当然,说相声并不会给科研带来直接帮助。“但是,如果不是相声以及相声社这个团体,我在疫情期间没法做实验的那段时候就太无聊了。靠着相声的调剂,我才在科研上完成了自己一直想完成的东西。”李泽阳说。
“我觉得平日里还最好能有一两个能够深入的爱好,哪怕看起来不务正业,但是作为调剂能给身心健康带来不少益处。”他继续说道。
 参考资料:
参考资料:1.Li, Z., Colombo, S., Shu, C., Velez, G., Pilatowsky-Cameo, S., Schmied, R., ... & Vuletić, V. (2023). Improving metrology with quantum scrambling.Science, 380(6652), 1381-1384.
2.Pedrozo, E., Colombo, E., Shu, S., Adiyatullin, A., Li, Z., … Vladan Vuletić, "Entanglement on an optical atomic-clock transition", Nature 588, 414-418, 2020. 2.
3.Colombo, S. Pedrozo, E., Adiyatullin, A., Li, Z., … Vladan Vuletić

好了,关于北大校友将量子信息暴散用于计量学,通过直观方式观察量子纠缠,可用于提高精密测量的准确度就讲到这。
版权及免责声明:凡本网所属版权作品,转载时须获得授权并注明来源“科技金融网”,违者本网将保留追究其相关法律责任的权力。凡转载文章,不代表本网观点和立场,如有侵权,请联系我们删除。
相关文章
- “尔森”用心倾听大自然的神秘邀约
- “考生”硕士统考发布报名提醒 考生需及时自查,抓紧时间修改
- “合肥市”“柿柿如意,柿如破竹”…… 高三学子“花式解压”
- “肌肉”磁铁刺激疗法可“对齐”肌肉纤维
- “低价”第15个双11:电商巨头争夺“最低价”、取消预售、开放生态
- “犯罪嫌疑人”湖南新化砍伤一对夫妇的犯罪嫌疑人落网,4人涉嫌窝藏罪被批捕
- “中国移动”中移动市场详情:合作伙伴大会重要发言及发布、反诈、5G应用获奖
- “血液”简单的血液检查调整可使重症监护治疗更安全
- “南充市”落马公安局长收受财物1365万被判7年:悔称利欲熏心,“金钱大厦”瞬间倾覆一生毁灭
- “高粱”河南固始有执法人员带人偷高粱?当地回应:涉事人员为行政执法大队人员,正调查
- “突触”我国科学家成功探测人工神经元突触的量子成像
- “量子”诺奖加持,量子点显示“钱”景几何
- “量子”《自然》(20231012出版)一周论文导读
- “突触”中国科大在人工神经元突触的量子成像取得重要进展
- “量子”“九章三号”光量子计算原型机来了
- “量子”“九章三号”光量子计算原型机研制成功,技术水平刷新世界纪录
- “量子”中国科大团队成功研制量子计算原型机“九章三号” 再度刷新世界纪录
- “量子”再度刷新世界纪录!“九章三号”光量子计算原型机研制成功
- “量子”百度发布首个量子领域大模型
- “黄山”价值1亿元:国盾量子科技园(二期)项目施工总承包开启招标









