“模型”既是自编码器，也是RNN，DeepMind科学家八个视角剖析扩散模型

今天，很高兴为大家分享来自机器之心Pro的既是自编码器，也是RNN，DeepMind科学家八个视角剖析扩散模型，如果您对既是自编码器，也是RNN，DeepMind科学家八个视角剖析扩散模型感兴趣，请往下看。

机器之心编译

作者：Sander Dieleman

编辑：Panda W

扩散模型很火，对其描述也大有不同。本文中，一位 DeepMind 研究科学家全面剖析了「扩散模型是什么」这一课题。

如果你尝试过目前最火的 AI 绘画工具之一 Stable Diffusion，那你就已经体验过扩散模型（diffusion model）那强大的生成能力。但如果你想更进一步，了解其工作方式，你会发现扩散模型的形式其实有很多种。

如果你随机选择两篇关于扩散模型的研究论文，看看各自引言中对模型类别的描述，你可能会看到它们的描述大不相同。这可能既让人沮丧，又具有启发性：让人沮丧是因为人们更难发现论文和实现之间的关系，而具有启发性的原因则是每一种观点都能揭示出新的联系，催生出新的思想。

近日，DeepMind 研究科学家 Sander Dieleman 发布了一篇博客长文，概括性地总结了他对扩散模型的看法。

这篇文章是他去年所写的《扩散模型是自动编码器》一文的进一步延伸。这个题目有些开玩笑的意味，但也强调了扩散模型和自动编码器之间存在紧密联系。他认为人们直到如今依然低估了这种联系。

感兴趣的读者可访阅：https://sander.ai/2022/01/31/diffusion.html

而在这篇新文章中，Dieleman 从多个不同视角剖析了扩散模型，包括将扩散模型看作是自动编码器、深度隐变量模型、预测分数函数的模型、求解逆向随机微分方程的模型、流模型、循环神经网络、自回归模型以及估计期望的模型。他还谈了自己对扩散模型研究方向的当前研究现状的看法。

扩散模型是自动编码器

去噪自动编码器是一种神经网络，其输入被噪声损伤，而它们的任务目标则是预测出干净的输入，即消除损伤。要很好地完成这一任务，需要学习干净数据的分布。它们是非常常用的表征学习方法，而在深度学习发展早期，它们也被用于深度神经网络的分层预训练。

事实证明扩散模型中使用的神经网络通常求解的是一个非常类似的问题：给定一个被噪声污染的输入示例，它要预测出与其数据分布相关的一些量。这可以是对应的干净输入（如同去噪自动编码器）、所添加的噪声或某种介于两者之间的东西（稍后会详细介绍）。当损伤过程是线性的时，所有这些都是等价的，即噪声是添加上去的，只需从有噪声输入中减去预测结果，我们就可以将预测噪声的模型变成预测干净输入的模型。用神经网络术语来说，就是从输入到输出添加一个残差连接。

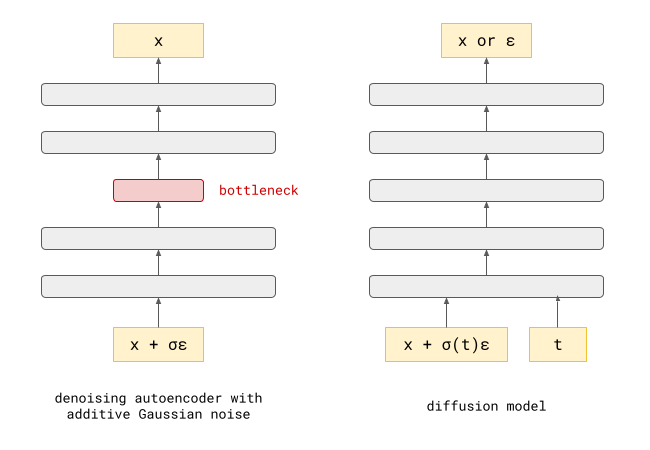
它们有几项关键性差异：

在学习输入的有用表征时，去噪自动编码器中部的某个位置往往存在某种信息瓶颈，这会限制其学习表征的能力。去噪任务本身只是达到目的的一种手段，而不是我们在训练模型后真正使用模型的目的。用于扩散模型的神经网络通常没有这样的瓶颈，因为我们更在乎它们的预测结果，而不是用于得到这些结果的内部表征方式。

去噪自动编码器可以使用多种不同类型的噪声来训练。比如说，我们可以将部分输入遮蔽掉（掩蔽噪声），我们也可以添加来自某个任意分布（通常是高斯分布）的噪声。对于扩散模型，我们通常坚持添加高斯噪声，因为它具有有用的数学特性，可以简化许多操作。

另一个重要差异是去噪自动编码器的训练目标只是处理特定强度的噪声。而使用扩散模型时，我们想要根据带有很多或少量噪声的输入预测一些东西。噪声水平也是神经网络的一个输入。

事实上，作者之前详细讨论过这两者之间的关系，想更加透彻理解这一关系的读者可访问：https://sander.ai/2022/01/31/diffusion.html

扩散模型是深度隐变量模型

Sohl-Dickstein et al. 在一篇 ICML 2015 论文中最早建议使用扩散过程来逐渐损伤数据的结构，然后再通过学习逆向该过程来构建生成模型。五年之后，Ho et al. 基于此开发出了去噪扩散概率模型（DDPM），其与基于评分的模型一起构成了扩散模型的蓝图。

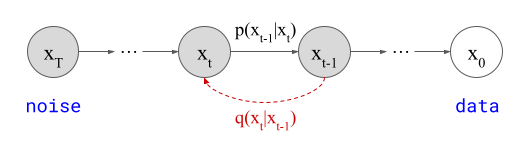
DDPM 如上图所示，x_T（隐含）表示高斯噪声，x_0（观察到的）表示数据分布。这些随机变量由有限数量的中间隐变量 x_t （通常 T=1000）连接在一起，这会形成一个马尔可夫链，即 x_{t-1} 仅取决于 x_t，而并不直接依赖于该链中之前的任意随机变量。

这个马尔可夫链的参数的拟合方式是使用变分推理来逆向扩散过程，这个扩散过程本身也是一个马尔可夫链（方向相反，图中表示为 q (x_t∣x_{t−1})），但这条链是逐渐向数据添加高斯噪声。

具体来说，就像是在变分自动编码器（VAE）中一样，我们可以写下一个证据下界（ELBO），即对数似然的一个界限，而对数似然是可以轻松地最大化的。事实上，这一节的小标题也可以是「扩散模型是深度 VAE」，但由于之前已经从另一个视角写了「扩散模型是自动编码器」，因此为了避免混淆就选用了当前小标题。

我们知道 q (x_t∣x_{t−1}) 是高斯分布，但我们想使用模型拟合的 p (x_{t−1}∣x_t) 却不需要是。但事实证明，只要每个单独的步骤足够小（即 T 足够大），我们可以通过参数设置让 p (x_{t−1}∣x_t) 看起来像是高斯分布，而且其近似误差将足够小，该模型依然能生成优质样本。仔细想想，这有点令人惊讶，因为在采样过程中，任何错误都可能随着 T 而累积。

扩散模型预测的是分数函数

大多数基于似然的生成模型都是对输入 x 的对数似然 log p (x∣θ) 进行参数化，然后拟合模型参数 θ 来最大化它，要么是近似地拟合（如 VAE），要么是精确拟合（如流模型或自回归模型）。由于对数似然表示概率分布，而概率分布必须归一化，所以通常需要一些约束来确保参数 θ 的所有可能值都产生有效的分布。比如自回归模型通过因果掩码（causal masking）来确保这一点，而大多数流模型需要可逆的神经网络架构。

研究表明，还有另一种拟合分布的方法可以巧妙地避开对归一化的要求，即分数匹配（score matching）。这基于这一观察：所谓的分数函数（score matching）

不会随 p (x∣θ) 的缩放而变化。这很容易看出来：

施加于概率密度的任何比例因子都会消失。因此，如果我们有一个直接对分数估计

进行参数化的模型，那就可以通过最小化分数匹配损失来拟合分布（而不是直接最大化似然）：

但是，使用这种形式时，损失函数可能不实用，因为我们没有为任意数据点 x 计算基本真值分数

的好方法。有一些技巧可用来回避这一要求，并将其转换为易于计算的损失函数，包括隐式分数匹配（ISM）、切片分数匹配（SSM）和去噪分数匹配（DSM）。这里我们详细看看最后一种方法：

其中，可通过向 x 添加高斯噪声得到

的分布基于一个高斯分布 N (x,σ^2)，其基本真值条件分数函数可以闭式形式计算得到：

。这意味着

这种形式有非常直观的解释：这是向 x 添加噪声以得到的一种扩展版本。因此，通过按照分数（= 对数似然的梯度上升）来使的可能性更高这一做法直接对应于消除（部分）噪声：

如果我们选择步长 η=σ^2，则就能在一步之内恢复干净数据 x。

L_SM 和 L_DSM 是不同的损失函数，但巧妙之处在于它们具有相同的期望最小值：

，其中 C 是一个常数。Pascal Vincent 早在 2010 年就推导出了这种等价性，如果你想加深理解，强烈建议你阅读他的技术报告：http://www.iro.umontreal.ca/~vincentp/Publications/smdae_techreport.pdf

这一方法引出了一个重要问题：我们应该添加多少噪声，即 σ 应为多少？为这一超参数选取一个固定值在实践中效果并不好。在低噪声水平下，在低密度区域中准确估计分数是非常困难的。在高噪声水平下，这算不上是一个问题，因为添加的噪声会分散在所有方向的密度上 —— 然后我们正在建模的分布会因噪声而显著扭曲。一种很好的方法是在许多不同噪声水平下建模密度。一旦我们有了这样一个模型，我们就可以在采样过程中对 σ 进行退火 —— 从大量噪声开始，然后逐渐降低。Song & Ermon 在他们 2019 年的论文中详细描述了这些问题并提出了这种优雅的解决方案。

这种方法是将多种不同噪声水平下的去噪分数匹配与采样期间噪声逐渐退火组合起来，得到的模型实质上等效于 DDPM，但推导过程却完全不同 —— 完全看不见 ELBO！

有关这一方法的更详细论述请参阅论文作者之一宋飏的博客：https://yang-song.net/blog/2021/score/

扩散模型求解的是逆向随机微分方程

前面两个看待扩散模型的视角（深度隐变量模型和分数匹配）考虑的是离散的和有限的步骤。这些步骤对应于不同的高斯噪声水平，我们可以写出一个单调映射 σ(t)，其步骤索引 t 映射到该步骤的噪声的标准差。

如果我们让步数趋于无穷大，则可以将这些离散的索引变量替换为区间 [0,T] 上的连续值 t，这可被解释为一个时间变量，即 σ(t) 现在描述的是噪声的标准差随时间的演变。在连续时间中，我们可以用以下随机微分方程（SDE）来描述逐渐向数据点 x 添加噪声的扩散过程：

该方程将 x 的无穷小变化与 t 的无穷小变化联系了起来，dw 表示无穷小高斯噪声，也被称为维纳过程（Wiener process）。f 和 g 分别称为漂移系数和扩散系数。f 和 g 的特定选择可得到用于构建 DDPM 的连续时间版本马尔可夫链。

SDE 将微分方程和随机变量组合到了一起，乍一看似乎有点生畏。幸运的是，我们不需要太多现有的先进 SDE 机制来理解这种视角可以如何用于扩散模型。然而，有一个非常重要的结果可供我们使用。给定一个像上面那样描述扩散过程的 SDE，我们可以写出另一个描述另一方向的过程的 SDE，即反转时间：

该方程还描述了一个扩散过程。

是时间依赖型分数函数。这种时间依赖性源自这一事实：噪声水平会随时间变化。

是逆向维纳过程，

解释这种情况的原因超出了本文的范围，感兴趣的读者可阅读宋飏等人为扩散模型引入基于 SDE 的形式化的原始论文《Score-Based Generative Modeling through Stochastic Differential Equations》。

具体来说，如果我们有一种方法，可以估计时间依赖型分数函数，那么我们可以模拟逆向扩散过程，从而从噪声开始的数据分布中抽取样本。我们可以再次训练一个神经网络来预测这个量，并将其插入到逆向 SDE 中以获得连续时间扩散模型。

在实践中，模拟这个 SDE 需要再次对时间变量 t 执行离散化，因此你可能想知道为什么要这么做。其巧妙之处就在于现在我们可以在采样时间决定该离散化，而且在我们训练好分数预测模型之前不必固定下来。换句话说，通过选择采样步骤数，我们无需修改模型，就能非常自然地权衡考虑采样质量和计算成本。

扩散模型是流模型

还记得流模型吗？流模型并非现如今常用的生成模型，主要原因可能是它们需要更多参数才能在性能上赶上其它模型。这是由于它们的表达能力有限：流模型中使用的神经网络需要是可逆的，并且其雅可比行列式的对数行列式必须易于计算，这就严重限制了可能的计算类型。

至少，离散的归一化流就是这种情况。连续的归一化流（CNF）也存在，并且通常的形式为用神经网络参数化的常微分方程（ODE），其描述的是数据分布中的样本与一个简单基础分布的对应样本之间的一个确定性路径。CNF 不受前面提到的神经网络架构约束的影响，但其原始形式需要用反向传播通过一个 ODE 求解器来训练。尽管可以使用一些技巧来更加高效地完成这件事，但这也可能会阻碍更多人使用它。

我们回顾一下扩散模型的 SDE 形式化，其描述的随机过程是将简单基础分布的样本映射到数据分布的样本。有趣的问题出现了：中间样本的分布 p_t (x) 是怎样的，又会怎样随时间变化？这由福克 - 普朗克方程（Fokker-Planck equation）控制。如果你想了解实践中的情况，请查看论文 Song et al. (2021) 的附录 D.1。

疯狂的来了：有一个 ODE 所描述的确定性过程的时间依赖型分布与该 SDE 所描述的随机过程的完全一样！这被称为概率流 ODE。不仅如此，它有一个简单的闭式形式：

该方程描述了前向和后向过程（只需翻转符号即可变换方向），注意时间依赖型分数函数依然在其中。要证明这一点，你可以写下该 SDE 和概率流 ODE 的福克 - 普朗克方程，然后做一些代数运算，你会发现它们其实是一样的，因此必定具有形同的解 p_t (x)。

请注意，该 ODE 描述的过程与该 SDE 并不一样，这也不可能，因为确定性的微分方程无法描述一个随机过程。它描述的是一个不同的过程，其具有独特的属性，即两个过程的分布 p_t (x) 是一样的。

这一现象揭示出了重要的意义：来自简单基础分布的特定样本与来自数据分布的样本之间存在双射映射。对于所有随机性都包含在初始基础分布样本中的采样过程 —— 一旦采样完成，基于此得到数据样本的过程就是完全确定性的。这也意味着我们可以通过前向模拟 ODE 来将数据点映射到其相应的隐含表征，然后操作它们，再通过后向模拟 ODE 将它们映射回数据空间。

由这个概率流 ODE 描述的模型是一个连续归一化流模型，但我们不必反向传播通过 ODE 也能训练它，使该方法的扩展性好得多。

我们竟然可以做到这一点，而不会改变模型的训练方式，是不是很神奇？我们可以将分数预测器插入到前一节提到的逆向 SDE 或这一节的 ODE 中，然后得到两个以不同方式建模同一分布的不同生成模型。是不是很炫酷？

不仅如此，概率流 ODE 还能让扩散模型实现似然计算，参见 Song et al. (2021) 的附录 D.2。这也需要求解 ODE，所以成本几乎和采样一样高。

由于以上原因，概率流 ODE 范式最近变得相当受欢迎。比如 Karras et al. 将其用作探究不同扩散模型设计选择的基础，本文作者也与其合作者在他们的扩散语言模型中使用了它。这也被泛化和扩展到了扩散过程之外，以学习任意一对分布之间的映射，形式包括流匹配（Flow Matching）、修正流（Rectified Flows）和随机插值（Stochastic Interpolants）。

旁注：DDIM 给出了另一种可为扩散模型获取确定性采样过程的方法，该方法基于深度隐变量模型视角。

扩散模型是循环神经网络（RNN）

从扩散模型采样涉及到使用神经网络反复进行预测并使用这些预测来更新「画布」，而这画布一开始全是随机噪声。如果我们考虑这个过程的完整计算图，它看起来很像循环神经网络（RNN）。RNN 中有一个隐藏状态会反复通过一个循环单元来获得更新，而这个循环单元由一个或多个非线性的已参数化的运算（比如 LSTM 的门控机制）构成。其中，隐藏状态就是画布，因此它位于输入空间中，并且其中的单元由我们为扩散模型训练的去噪神经网络构成。

RNN 的训练通常使用通过时间的反向传播（BPTT），其中梯度是通过循环传播的。反向传播通过的循环步骤数通常受限于某个最大值，以降低计算成本，这被称为截断式 BPTT。扩散模型也是通过反向传播训练，但一次仅通过一步。从某种意义上说，扩散模型提供了一种训练深度循环神经网络的方法。该方法完全无需通过循环进行反向传播，从而可得到更具可扩展性的训练过程。

RNN 通常是确定性的，因此这个类比对于基于上一节中描述的概率流 ODE 的确定性过程最有意义 —— 尽管将噪声注入 RNN 的隐藏状态作为正则化的一种方法并非是前所未闻的事情，所以作者认为这个类比也适用于随机过程。

在非线性层的数量方面，这个计算图的总深度是由神经网络的层数乘以采样步骤数给定的。我们可以将展开的循环看作是一个非常深的神经网络，甚至可能有成千上万层。深度很大，但也说得过去，因为对真实世界数据进行生成式建模就需要如此深度的计算图。

我们还可以想想，如果我们在每个扩散采样步骤不使用同样的神经网络，对于不同的噪声水平范围可能使用不同的神经网络，那么会发生什么？这些网络可以单独且独立地训练，甚至可以使用不同的架构。这意味着我们可以有效地「解开」非常深的神经网络中的权重，将其从一个 RNN 变成一个普通的老式深度神经网络，但我们仍然无法避免一次性反向传播通过它们全部。Stable Diffusion XL 在其 Refiner 模型中使用这种方法达到了很好的效果，所以这种方法的热度可能会赶上来。

作者表示他在 2010 年开始读博时，训练隐藏层超过 2 层的神经网络可是个苦累活：反向传播不是一拿出来就好用，因此他们的做法是使用无监督的逐层预训练来寻找一个能够让反向传播成为可能的优良初始化。现如今，即使有数百隐藏层，也不再是阻碍。因此，不难想象未来几年之后，使用反向传播训练数万层的神经网络也有可能实现。到那时，扩散模型提供的「分而治之」的方法可能会失去光彩，也许我们都会回头去训练深度变分自动编码器！（注意，同样的「分而治之」视角也适用于自回归模型，因此如果未来果真如此，那么自回归模型也可能会过时。）

这一视角下的一个问题是：如果我们反向传播通过采样过程两步或更多步，扩散模型的表现是否会更好。这种方法并不常见，这可能说明这种方法实际做起来成本很高。不过也有一个重要的例外（一定程度上的例外），循环接口网络（RIN）等使用自调节（self-conditioning）的模型除了会在扩散采样步骤之间传递更新的画布之外，还会传递某种形式的状态。要让模型学会使用这个状态，可以在训练期间通过运行额外的前向传递来提供该状态的近似值。不过，这里不会有额外的向后传递，所以这实际上不算是两步 BPTT—— 更像是 1.5 步。

扩散模型是自回归模型

对于自然图像的扩散模型，采样过程往往会首先产生大尺度的结构，然后迭代地添加越来越细粒的细节。事实上，噪声水平与特征尺度之间似乎有近乎直接的对应关系。

但为什么会这样呢？为了理解这一点，从空间频率的角度思考会有所帮助。图像中的大尺度特征对应于低空间频率，而细粒度细节对应于高频率。我们可以使用 2D 傅立叶变换（或其某种变体）将图像分解为其空间频率分量。这通常是图像压缩算法的第一步，因为众所周知人类视觉系统对高频不太敏感，压缩时可以利用这一点，即更多地压缩高频，更少地压缩低频。

自然图像以及许多其它自然信号的频域会表现出一个有趣的现象：不同频率分量的幅度往往与频率的倒数成比例下降：

（如果你看的是功率谱而不是幅度谱，那么就是频率平方的倒数）。

另一方面，高斯噪声的谱形很平坦：在期望中，所以频率的幅度一样。由于傅里叶变换是线性运算，因此向自然图像添加高斯噪声会产生新图像，其频谱是原始图像的频谱与噪声的平坦频谱之和。在对数域中，两个光谱的叠加看起来像一个铰链，它表明添加噪声会以某种方式模糊更高空间频率中存在的任何结构（见下图）。这个噪声的标准差越大，受影响的空间频率就越多。

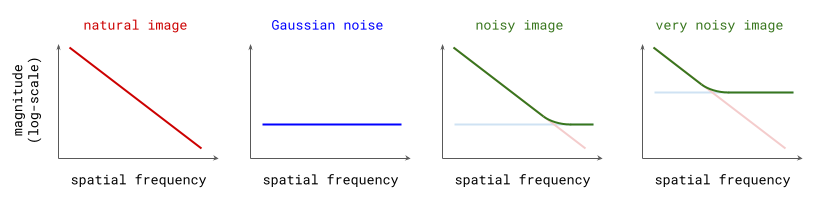
由于扩散模型的构建方式是逐渐向输入样本添加更多噪声，我们可以说这个过程会逐渐淹没越来越低频的内容，直到清除所有结构（至少对自然图像来说是这样的）。当从模型采样时，就调转方向，在越来越高的空间频率上有效地添加结构。这基本上就和自回归一样，却是在频率空间！Rissanen et al. (2023) 讨论了他们在使用逆向散热（inverse heat dissipation，这是高斯扩散的一种替代方法）的生成式建模方面观察到这一现象，但他们并未将其与自回归模型联系起来。这种联系是本文作者自己提出的，可能会具有争议。

一个重要的警告是：这种解释依赖于自然信号的频率特征，因此对于扩散模型在其它领域的应用（如语言建模），这种类比可能没有意义。

扩散模型估计的是期望

转移密度（transition density） p (x_t∣x_0) 描述的是：基于原始的干净输入 x_0，其衍生（通过添加噪声）出的有噪声数据示例 x_t 在时间 t  的分布。扩散模型中神经网络的任务是基于这一分布的样本预测其期望 E [x_0∣x_t]（或期望的某个线性的时间依赖型函数）。这可能看起来再明显不过，但这也能说明一些东西，这里强调一下。

首先，这提供了一个佐证，说明训练扩散模型时使用均方误差（MSE）作为损失函数是正确的选择。在训练期间，期望 E [x_0∣x_t] 是未知的，所以我们使用 x_0 本身来监督模型。因为 MSE 损失的最小值正是期望值，所以我们最终可以恢复 E [x_0∣x_t]（的近似值），即使我们事先不知道这个量。这和典型的监督学习问题有些不同。对于典型的监督学习问题，理想的结果是模型能准确预测出用于监督的目标（排除任何标注错误）。这里，我们故意不希望这样。更一般而言，估计条件期望的概念（即便我们只是通过样本提供监督）是非常强大的。

其实，这解释了为什么扩散模型的蒸馏是一个如此引人注目的命题：在这种情况下，我们可以直接使用我们希望预测的目标期望 E [x_0∣x_t] 的近似值来监督扩散模型，因为教师模型已经提供了这一点。由此导致的结果是，其训练损失的方差将远远低于从头开始训练时的情况，收敛速度也会快得多。当然，只有当你手上已经有一个已训练好的模型可用作教师时，这才会有用。

离散和连续的扩散模型

到目前为止，我们已经从几个视角考虑了一些离散噪声水平的情况，也有几个视角使用了连续时间概念，其与映射函数 σ(t) 相组合，可将时间步骤映射到噪声中对应的标准差。这些通常分别被称为离散时间或连续时间。一件非常巧妙的事情是：这主要就是一个如何解释的问题：在离散时间视角下训练的模型通常可以很容易地重新调整用途，以在连续时间设置中生效，反之亦然。

看扩散模型是离散还是连续的另一种方式是看输入空间。作者发现，文献中常常不会清楚说明「连续」或「离散」是相对于时间还是相对于输入。这非常重要，因为某些视角仅对连续输入才真正有意义，因为它们依赖于输入的梯度（即基于分数函数的所有视角）。

离散性 / 连续性存在四种组合方式：

时间离散，输入连续：原始的深度隐变量模型视角（DDPM）以及基于分数的视角；

时间连续，输入连续：基于 SDE 和 ODE 的视角；

时间离散，输入离散：D3PM、MaskGIT、Mask-predict、ARDM、多项式扩散和 SUNDAE 都是对离散输入使用迭代式精细化的方法 —— 是否所有这些都应该被视为扩散模型尚不完全清楚（这取决于你提问的对象）；

时间连续，输入离散：连续时间马尔可夫链（CTMC）、基于分数的连续时间离散扩散模型和 Blackout Diffusion 都是搭配了离散输入和连续时间 —— 这一设置通常的处理方式是将离散数据嵌入到欧几里得空间中，然后在该空间中对输入执行连续的扩散，例如 Analog Bits、Self-conditioned Embedding Diffusion 和 CDCD。

其它形式

最近有些论文基于第一性原理为这类模型提出了新的推导方式，由于已有后见之明，所以它们完全避开了微分方程、ELBO 或分数匹配。然而，这些研究为扩散模型提供了另一种视角，这可能更容易理解，因为所需的背景知识更少。

通过直接迭代进行反演（InDI/Inversion by Direct Iteration）这种形式根植于图像恢复，其目的是利用迭代式精细化来提升感知质量。其没有对图像劣化的本质做任何假设，并且模型的训练使用的是配对的低质量和高质量样本。Iterative α-(de) blending 通过在来自两个不同分布的样本之间进行线性插值作为起点，来得到这两个分布之间的确定性映射。这两种方法都与之前讨论的流匹配、修正流和随机插值方法紧密相关。

一致性

近期的文献对扩散模型的一致性（consistency）有着不同的概念。

一致性模型（CM）被训练用于将概率流 ODE 的任何轨迹上的点映射到轨迹的原点（即干净的数据点），从而实现在单一步骤中完成采样。其完成方式是间接的，即通过在特定轨迹上获取成对的点并确保模型对于两者的输出结果一样（因此有一致性）。其有一个蒸馏式的变体，它是从已有的扩散模型开始的，但也可能从头开始训练出一致性模型。

一致扩散模型（CDM）的训练使用了明确鼓励一致性的正则化项，其将一致性定义为：去噪器的预测结果应当对应于条件期望 E [x_0∣x_t]。

FP-Diffusion 的任务是让福克 - 普朗克方程描述 p_t (x) 随时间的演变，其中引入了一个显式的正则化项以确保其成立。

对理想的扩散模型（完全收敛又能力无限）而言，这些属性中的每一个都很容易实现。但是，现实中的扩散模型都是近似模型，并不是理想模型，所以它们在实践中并不成立，所以需要通过新增机制来显式地施行它们。

本文之所以有这一节，是因为作者想重点说明近期的一篇论文《On the Equivalence of Consistency-Type Models: Consistency Models, Consistent Diffusion Models, and Fokker-Planck Regularization》，来自 Lai et al. (2023)，其中表明这三种不同的一致性概念本质上是不同视角下的同一东西。作者表示这个结果很优雅，非常契合本文的主题。

打破常规

除了这些在概念层面上的不同视角，作者表示，扩散模型方面的论文也在重新发明符号和违反惯例方面特别令人担忧。有时候，对于同一概念，人们使用的两套描述看起来简直像是一点关系都没有。这无益于人们理解和学习，提高了进入门槛。（对此我很抱歉。）

还有一些其它看似无害的细节和参数化选择也可能产生深远影响。以下是需要注意的三点：

总的来说，人们使用的是方差保持（VP/variance-preserving）扩散过程，即除了在每一步添加噪声，当前画布的尺寸也会得到调整以保持整体的方差。不过，方差爆炸（VE/variance-exploding）方法也有不少拥趸，其中不会调整画布尺寸，所添加的噪声的方差会无限增大。最值得注意的是 Karras et al. (2022) 使用的方法。某些对于 VP 扩散方法成立的结果对 VE 扩散就不一定成立，反之亦然；并且这一点可能不会被明确提及。如果你在读一篇扩散论文，要确保你知道所使用的构建方法，以及论文中是否做了有关于其的假设。

有时扩散模型中使用的神经网络的参数被设计成为了预测添加到输入中的（标准化）噪声，即分数函数，有时则是为了预测干净的输入或甚至这两者的时间依赖型组合（如 v-prediction）。所有这些目标都是等效的，因为它们都是彼此和有噪声输入 x_t 的时间依赖型线性函数。但重要的是，要了解其与训练期间不同时间步骤的损失贡献的相对权重的作用方式，这会极大影响模型的性能表现。对于图像数据而言，预测标准化噪声似乎是个绝佳选择。人们发现，当建模其它某些量（如隐含扩散中的隐含量）时，预测干净输入的效果更好。这主要是因为它暗含了对噪声水平的不同加权，因此特征尺度也就不同。

人们普遍认为，损伤过程所添加的噪声的标准偏差会随时间而增加，即熵会随时间增加，就像我们的宇宙。因此，x_0 对应于干净数据，x_T（当 T 足够大时）对应于纯噪声。流匹配等一些研究颠倒了这种惯例，如果你一开始没注意到，可能会深感困惑。

最后，值得注意的是，在生成式建模的语境下，「扩散」的定义范围已经变得相当广泛，现在几乎就等同于「迭代式精细化」。许多用于离散输入的「扩散模型」实际上并不基于扩散过程，但是它们当然是紧密相关的，因此扩散这一标签的范围会逐渐扩大并将它们囊括进来。界线在哪目前尚未可知：如果通过逆向逐渐损伤的过程而实现迭代式精细化的任何模型都算是扩散模型，那么所有自回归模型也算是扩散模型。作者认为，这样就太混淆了，会让「扩散」这个术语变得毫无用处。

结语

目前，学习有关扩散模型的知识肯定很让人困惑，但对这些不同视角的探索已经催生出了广泛多样的方法和工具，这些方法可以组合起来使用，毕竟其底层模型都是一样的。另外，了解这些不同视角的相关性还能加深理解。在一个视角下看起来神秘难解的东西在另一个视角看来可能就很明晰。

如果你才刚开始学习扩散模型，希望这篇文章能为你提供引导，帮助你找到更进一步的学习材料。如果你已经经验丰富，也希望这篇文章能拓宽你对扩散模型的理解，让你温故而知新。感谢阅读！

对于扩散，你最喜欢的视角是哪一个？文中还没提到哪些有用的视角？请与我们分享你的看法。

博客地址：https://sander.ai/2023/07/20/perspectives.html#fn:sde

好了，关于既是自编码器，也是RNN，DeepMind科学家八个视角剖析扩散模型就讲到这。